In order to analyze x-mas-3 and training an AI to play the game, we decided to make an abstract version in the game in R (R Core Team 2023) and C++ (ISO 2012). The abstracted version is more suitable for computer-game interaction as it will communicate only the relevant information between the agent and the game. This will be substantially faster than interacting with the UI and allow for a more streamlined training process.
The board is a 6 by 10 grid each containing a tile out of ten different tile-types. For our purposes we represent the board as a 6x10 matrix with the letters A through J representing the ten different tiles. An example board would me represented thus:
\[\begin{bmatrix} G & C & J & D & G & G & C & G & B & A \\ I & D & E & A & C & B & H & C & E & F \\ J & C & J & F & C & J & A & H & B & F \\ H & C & D & F & C & F & D & B & G & B \\ D & I & H & I & I & B & F & C & C & E \\ B & F & A & J & E & H & I & C & H & G \end{bmatrix}\]Using this structure we can check for the presence of combinations using regular expressions. Using
\[ \text{([A-J])\\1\\1+} \]
as a regular expression will identify three or more consecutive occurrences of similar tiles. Implemented in R below:
get_n_combinations <- \(m){
my_regex <- "([A-J])\\1\\1+"
rowmatch <- purrr::map_lgl(1:6,~{
my_str <- stringr::str_c(m[.x,], collapse = "")
grepl(my_regex,my_str)
})
colmatch <-purrr::map_lgl(1:10,~{
grepl(my_regex,stringr::str_c(m[,.x], collapse = ""))
})
sum(colmatch,rowmatch)
}In this case one match is returned because of the triple “C”s found in column 5.
Since the initial state of the board cannot include any scoring combination we need a function that generates a random initial state until the board’s score is zero. We implemented this recursively.
initialize_board <- \(){
tiles <- LETTERS[1:10]
board <- matrix(data = sample(tiles,60,replace = TRUE),6,10)
## If the initial state scores, generate another one
if(get_n_combinations(board)>0){
board <- initialize_board()
}
board
}
initialize_board()Moves are made by specifying a cell, (by clicking on it) and then switching it with one of it’s neighbors directly above, below, to the left or to the right. When a move is made the neighboring tile switches places with the first one clicked.
Reinforcement Learning (RL) (Watkins and Dayan 1992) is an algorithm that allows an agent (i.e. AI) to interact with an environment over a sequence of observations. The agent seeks to be rewarded and for the reward to be maximized over time. The model consists of a set of environment states \(S\) a set of actions \(A\) and a set of rewards \(R\) (positive or negative).
The algorithm is guaranteed to converge to an optimal policy for each possible state in \(S\). RL (and in this case we will use Q-learning) needs to be trained on a set of state-transition tuples formally defined in eq-tuples. \[ (s_i, a_i, r_{i+1}, s_{i+1}) \tag{2.1}\]
where:
For \(S\) we have ten possibilities for each of the 60 (\(6\times10\)) cells on our board. For \(A\) the agent can make one out of four moves in each of the 60 cells (ignoring for the moment the marginal cases of moving off the board, which is not possible). As for the reward space \(R\), this can probably be set to the actual scores of the game, with some smaller penalty for making a non-scoring move or Passing (subsequent analysis will make it clear why this needs to be a possibility for practical purposes).
For our \(S\) as defined above the number of possible states is \(10^{60}\), which is a 1 followed by 60 zeros, i.e.:
|\__/,| (`\
_.|o o |_ ) )
---(((---(((---------Wow, that's a huge number!\(10^{60}\) = 1,000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000.
The action space \(A\) is slightly smaller since there are only four possibilities for each cell, so we have “only” \(4^{60}\) which is roughly equal to \(1.329\times10^{36}\).
Given the magnitude of these numbers it is clear that we cannot reasonably expect the algorithm to converge for several millennia with the computing power currently at our disposal. We therefore need to employ some strategies for reducing the spaces.
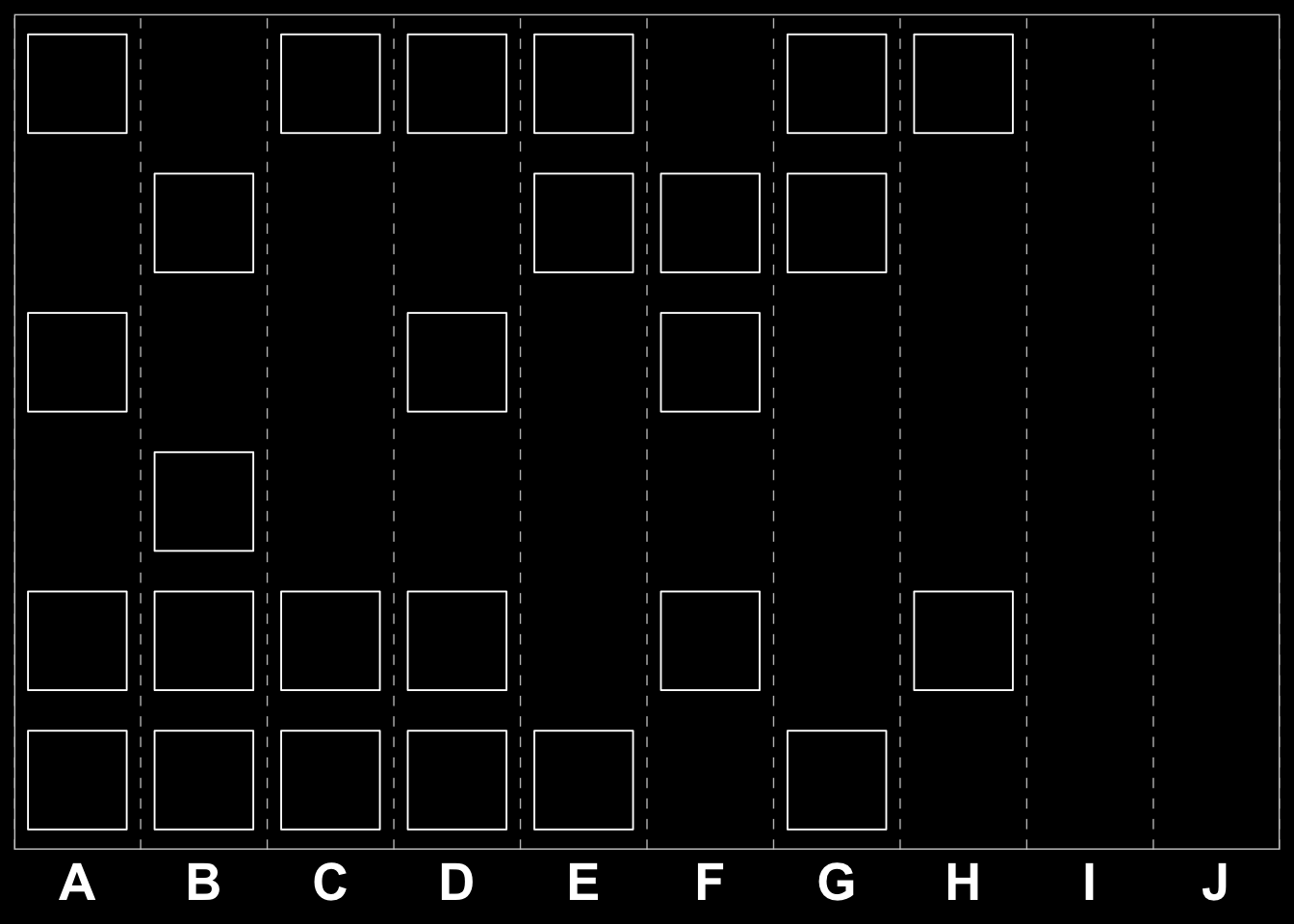
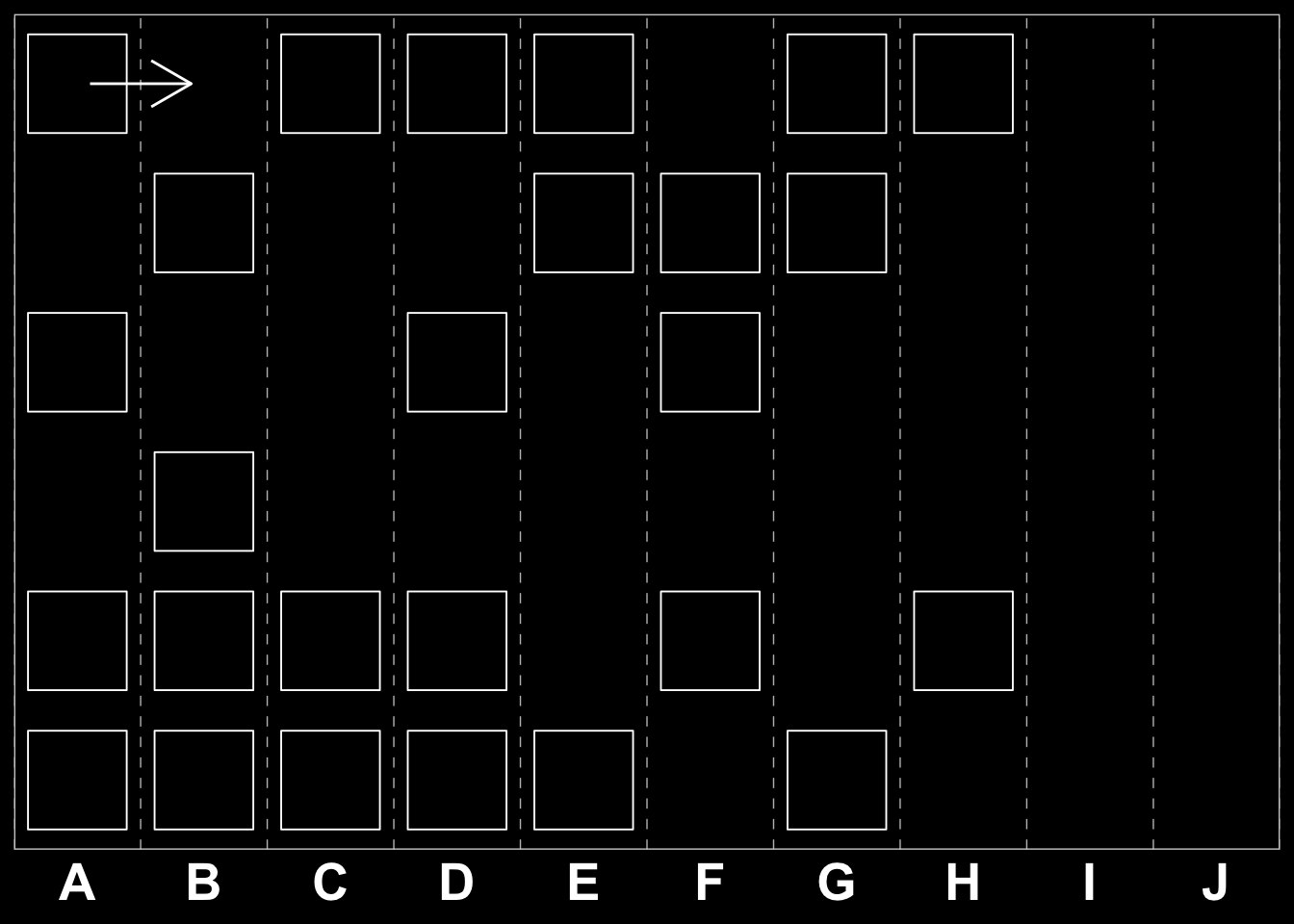
We can consider a one-type-at-a-time strategy. The heuristic implemented would then be to first look for moves involving candy, then move on to trees and so on. For example: staring with an initial board like this:
\[\begin{bmatrix} G & C & J & D & G & G & C & G & B & A \\ I & D & E & A & C & B & H & C & E & F \\ J & C & J & F & C & J & A & H & B & F \\ H & C & D & F & C & F & D & B & G & B \\ D & I & H & I & I & B & F & C & C & E \\ B & F & A & J & E & H & I & C & H & G \end{bmatrix}\]And chose to consider the “A” cells we get:
\[\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \end{bmatrix}\]This reduces the problem to a binary one and we effectively reduce \(S\) to \(2^{60}\), which is merely 1.15 quintillions. While this represents a huge reduction, it is still far from being feasible. In addition this does not reduce our action space \(A\), as you still have four possible moves for each of the 60 cells.
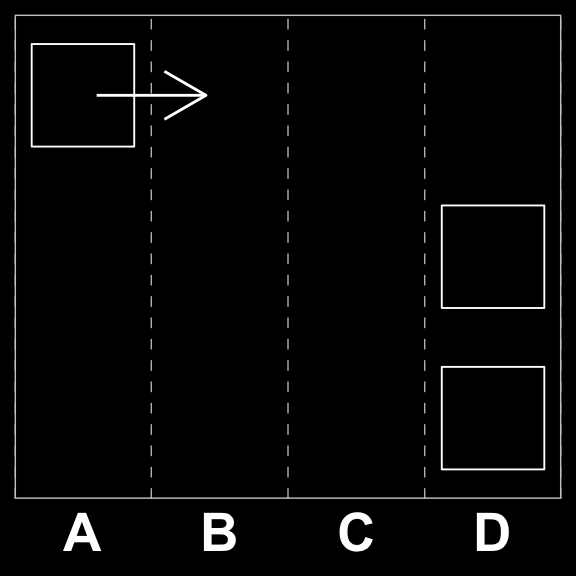
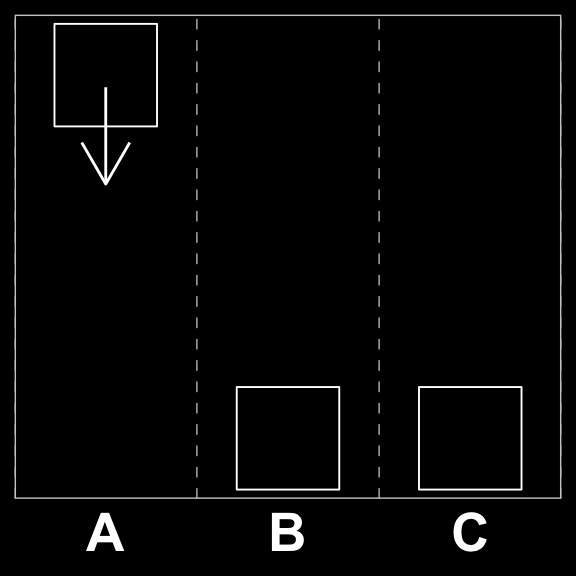
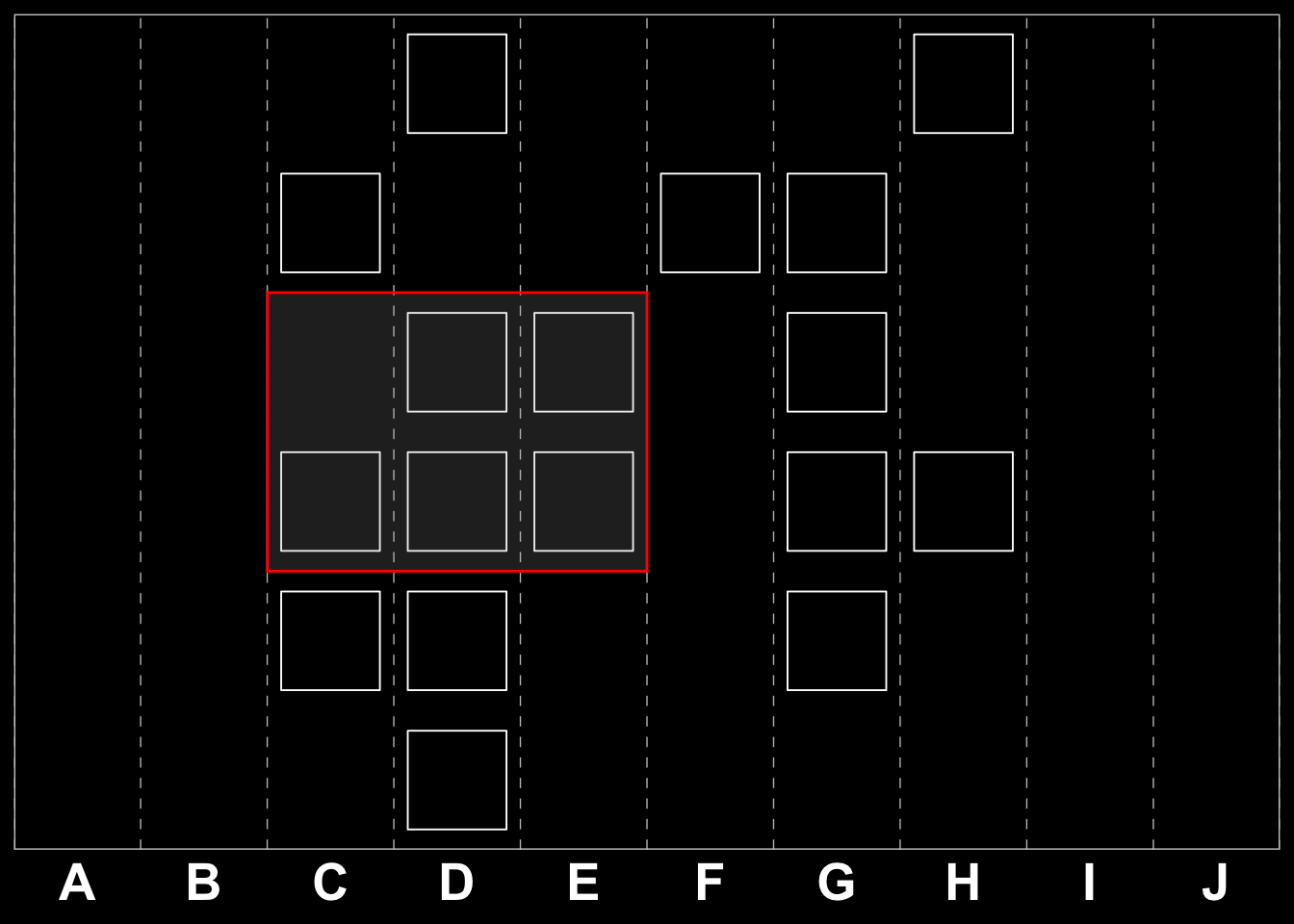
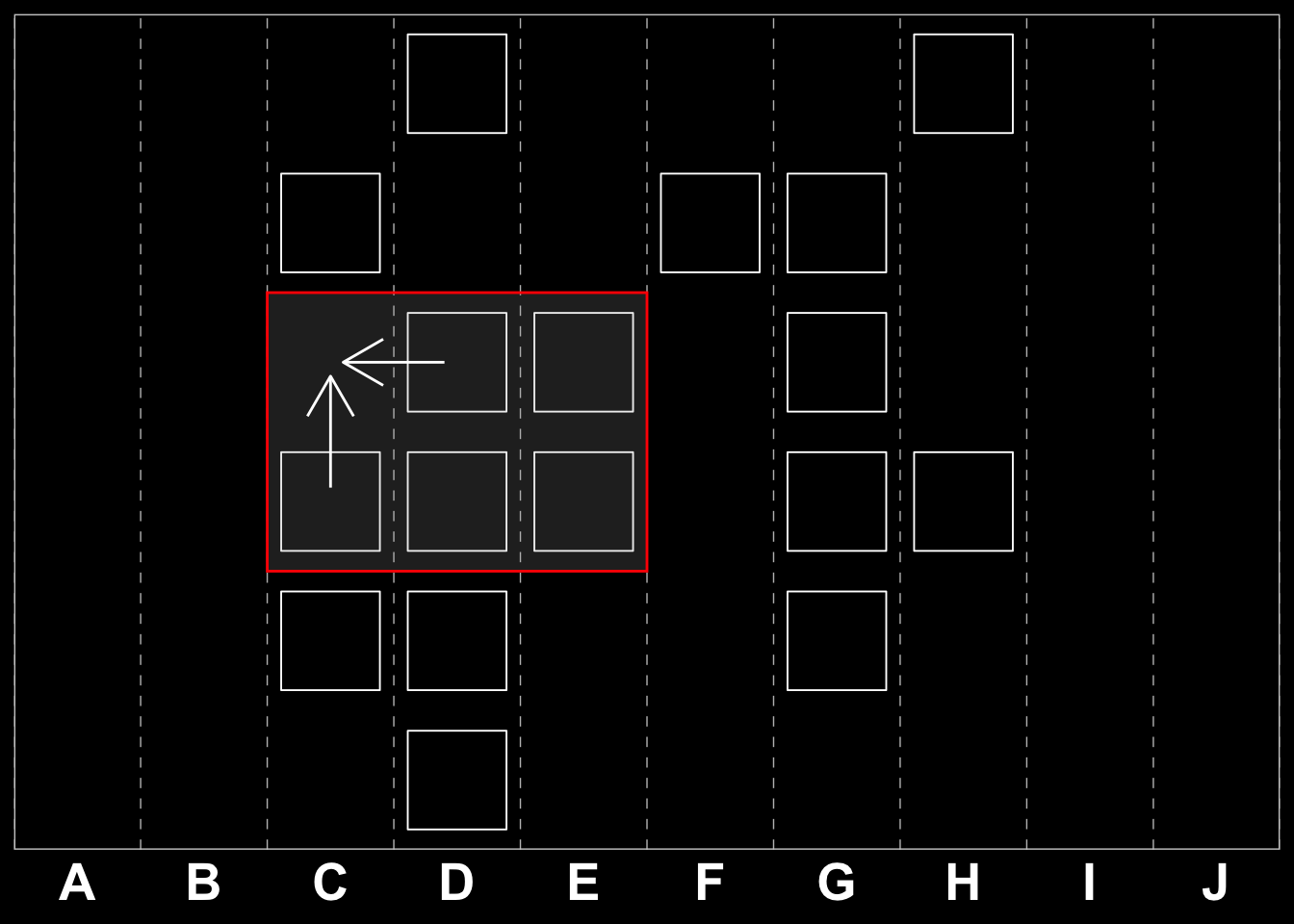
We can further reduce our problem space by applying a technique known as windowing. This implies dividing the grid into sub-grids and looking for playable moves within those reduced spaces. If we first consider the quest for a three-tile combinations, the windows in question would be a \(3\times2\) and a \(2\times3\) sub-matrix for perpendicular (\(\perp\))moves. For parallel (\(\parallel\)) moves, i.e. moves with the same row or column we would have to consider \(1\times4\) and \(4\times1\) respectively. Examples are shown below.
\[\begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} % \text{ or} % \begin{bmatrix} 1 & 0 \\ 1 & 1 \\ 0 & 1 \end{bmatrix} % \text{ for }\perp\text{moves,}\]and
\[\begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} % \text{ or} % \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} % \text{ for }\parallel \text{ moves.}\]Is it easy to see that the \(3\times2\) matrix above is a transposition of the \(2\times3\) one, and therefore it does not matter whether a move if horizontal or vertical the problem is similar in nature for all perpendicular moves. The same is true for the \(4\times1\) and \(1\times4\) matrices, i.e. where there is a winning parallel move. Matrix eq-example-windows illustrates two windows on our original board and Matrix eq-example-windows-binary shows the same in our binary space (combining the two reduction strategies).
\[ \begin{bmatrix} G & \color{red}{\textbf{C}} & \color{red}{\textbf{J}} & \color{red}{\textbf{D}} & \color{red}{\textbf{G}} & G & C & G & B & A \\ I & D & E & A & C & B & H & C & E & F \\ J & C & J & F & C & J & \color{red}{\textbf{A}} & \color{red}{\textbf{H}} & B & F \\ H & C & D & F & C & F & \color{red}{\textbf{D}} & \color{red}{\textbf{B}} & G & B \\ D & I & H & I & I & B & \color{red}{\textbf{F}} & \color{red}{\textbf{C}} & C & E \\ B & F & A & J & E & H & I & C & H & G \end{bmatrix} \tag{2.2}\]
\[ \begin{bmatrix} 0 & \color{red}{\textbf{1}} & \color{red}{\textbf{0}} & \color{red}{\textbf{0}} & \color{red}{\textbf{0}} & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & \color{red}{\textbf{0}} & \color{red}{\textbf{0}} & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & \color{red}{\textbf{0}} & \color{red}{\textbf{0}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \color{red}{\textbf{0}} & \color{red}{\textbf{1}} & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{bmatrix} \tag{2.3}\]
If we employ the windowed approach suggested above, our action space, \(A\) shrinks significantly. We will in fact have two different \(S\) and \(A\) depending on whether we are considering parallel or perpendicular moves.
For a parallel window, we can generalize to the horizontal variant (since the horizontal one is a simple transposition thereof) and we then get only a few relevant combinations. Since any four element set which already has three in a row is will not occur, we are left with: {0000,0001,0010,0011,0100,0101,0110,1000,1001,1011, 1101} for a total of 11 cases out of which only two have a winning move ({1011, 1101}). This reduces \(A_{\parallel}\) for \(S_{\parallel}\) to three moves: pass (P), flip first (F) or flip last (L). formalized in Equation eq-action-space-parallel.
\[ A_{\parallel} = \{P,F,L\} \tag{2.4}\]
For the perpendicular case we 62 combinations, these are illustrated in Equation eq-perpendicular-combinations.
\[ S_{\perp} = \Biggl\{ \left[{000\atop{000}}\right], \left[{000\atop{001}}\right], \left[{000\atop{010}}\right] ... \left[{001\atop{001}}\right], \left[{001\atop{010}}\right]... \left[{110\atop{011}}\right] \Biggr\} \tag{2.5}\]
The action space is limited to flipping one out of three positions, First, Middle, Last, or Passing. Illustrated in Equation eq-action-space-perpendicular.
\[ A_{\perp}=\{F,M,L,P\} \tag{2.6}\]
The windowed approach proposed above, along with the one-type-at-a-time technique reduce our \(A\) and \(S\) to magnitudes that are manageable and allow us to generate a training set. They do limit the potential for the agent in some non-trivial ways, namely:
In view of (2) the more precise description of our endeavor is perhaps to say that we are teaching it tactics rather than strategy.
We will later see if it is feasible to generalize this approach and create larger grids.
In order to facilitate the discussion and analysis of positions and moves I decided to use notation inspired by algebraic notation in the game of chess. Our board is 6x10 (as opposed to 8x8 in chess), so we have columns A through J, and rows 1 through 6. Since there is a component of “gravity” in the game, i.e. tiles fall toward the botton of the screen when tiles are removed from the board, I decided to number rows from the top. This would be congruent with the typical layout of a chess board, but seen from the perpective of the black pieces. An example can be seen in Figure fig-example-board-algebraic-notation.
Moving the top-left tile to the adjecent square to the right would be denoted: “A1 to B1” or simply “A1B1”. The move is illustrated in Figure fig-example-move.
Since the strategies and tactics learned on a i.e. 3x4 board are in principle the same as those of a 4x3 board it is useful to be able to transpose both boards and moves. We therefore implemented transpose-functions for both.
Another class of transpositions applies to those that are either horizontal or vertical, but do not imply a flip around the matrix’s diagonal. For the avoidance of confusion I chose to denominate these operations as sliding. And the origin area of a slide a window.
Since we are operating on simplified sub-boards, and part of our strategy is to window the playing-board we implemented functions to window a board, i.e. subdivide it into smaller pieces for analysis. When moves are suggested for the sub-division we need to slide these moves over on the real playing board (i.e. the larger one).
