4  Full Board Strategies

4.1 Applicable Models

From the model training already performed we have a total of six models: 3x3, 3x4, 3x5, 3x6 and 4x4, for sub-boards (windowed grids) as well as their relevant transpositions. Any of these can be used to scan the entire board looking for playable moves or move sequences (i.e. strategic moves) by using the windowing technique already described. Each evaluation of a sub-boards will return a best move or move-sequence and expected value of the sequence (which may be of cardinality 1). We may have some intuition about which strategy is optimal, e.g. all 3x3 sub-boards are included in a series of other geometries (3x4, 3x5, 3x6 and 4x4), and the best strategy can be derived mathematically. We chose the statistics route to the optimal strategy.

4.2 Monte Carlo Simulations

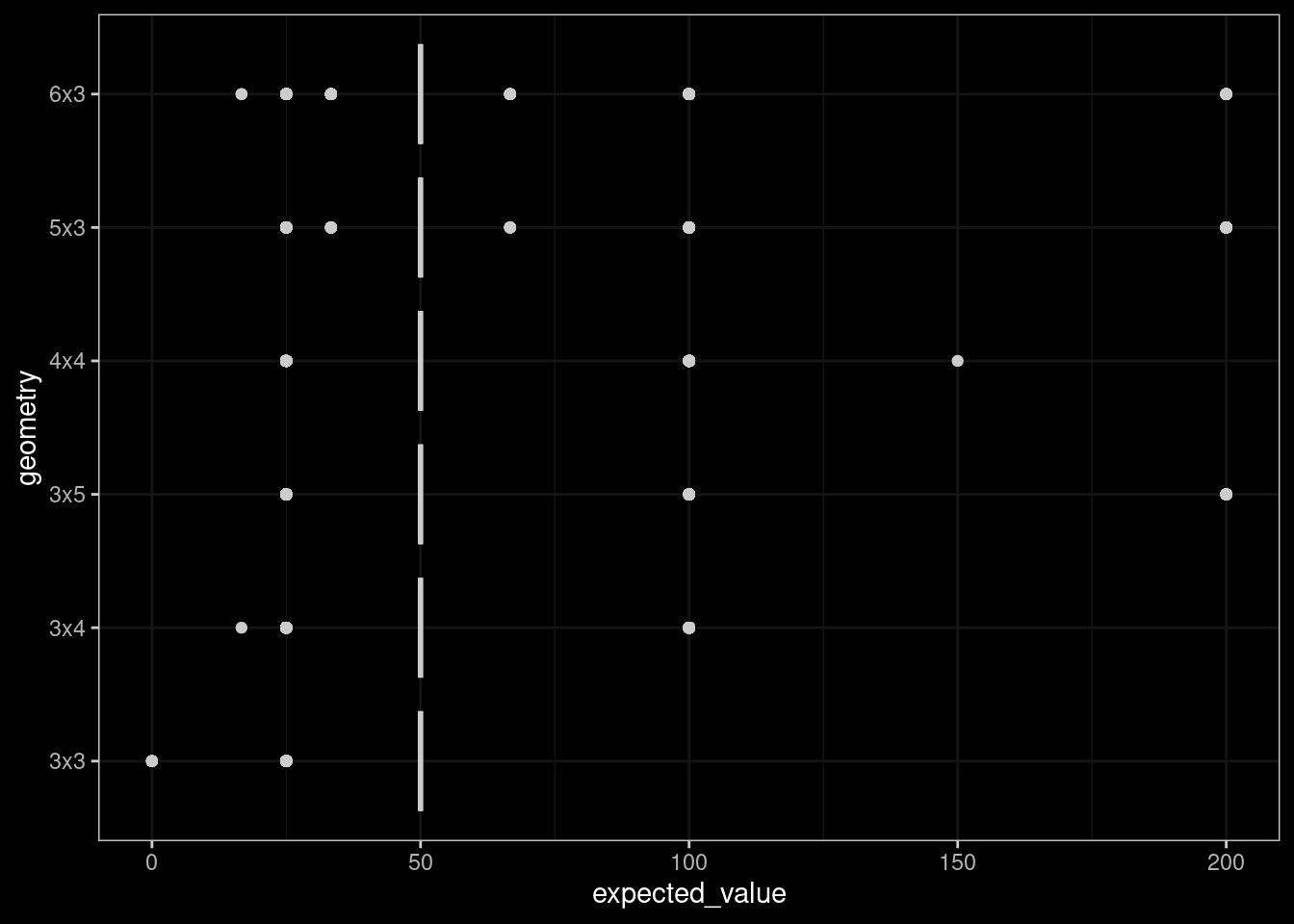
We conducted Monte Carlo simulations of ten thousand (10,000) random boards, each played with each of the available geometries. This is the equivalent of playing 100 games (in arcade mode) with each strategy. The score on the move, number of moves and expected score per move (relevant if strategic moves are made) were calculated as well. The summary statistics are shown in Figure 4.1 and Table 4.1 respectively.

Figure 4.1: Boxplot of Expected Values for the ‘Best Move’ Strategy, by Geometry

Table 4.1: Expected Score by Geometry

geometry	Median	Mean	SD
3x3	50	48.880	5.244
3x4	50	50.394	8.087
3x5	50	52.312	13.114
4x4	50	53.680	14.004
5x3	50	52.928	14.743
6x3	50	52.075	14.221

We can see that the 4x4 geometry is marginally superior when using the best move strategy.

Time of Evaluation

As we will be developing full board strategies for both arcade and time mode in the actual game, we also analyzed the time it took Gatai to evaluate the boards using each of the geometries. The results are shown in Figure 4.2.

Figure 4.2: Time per Move by Geometry

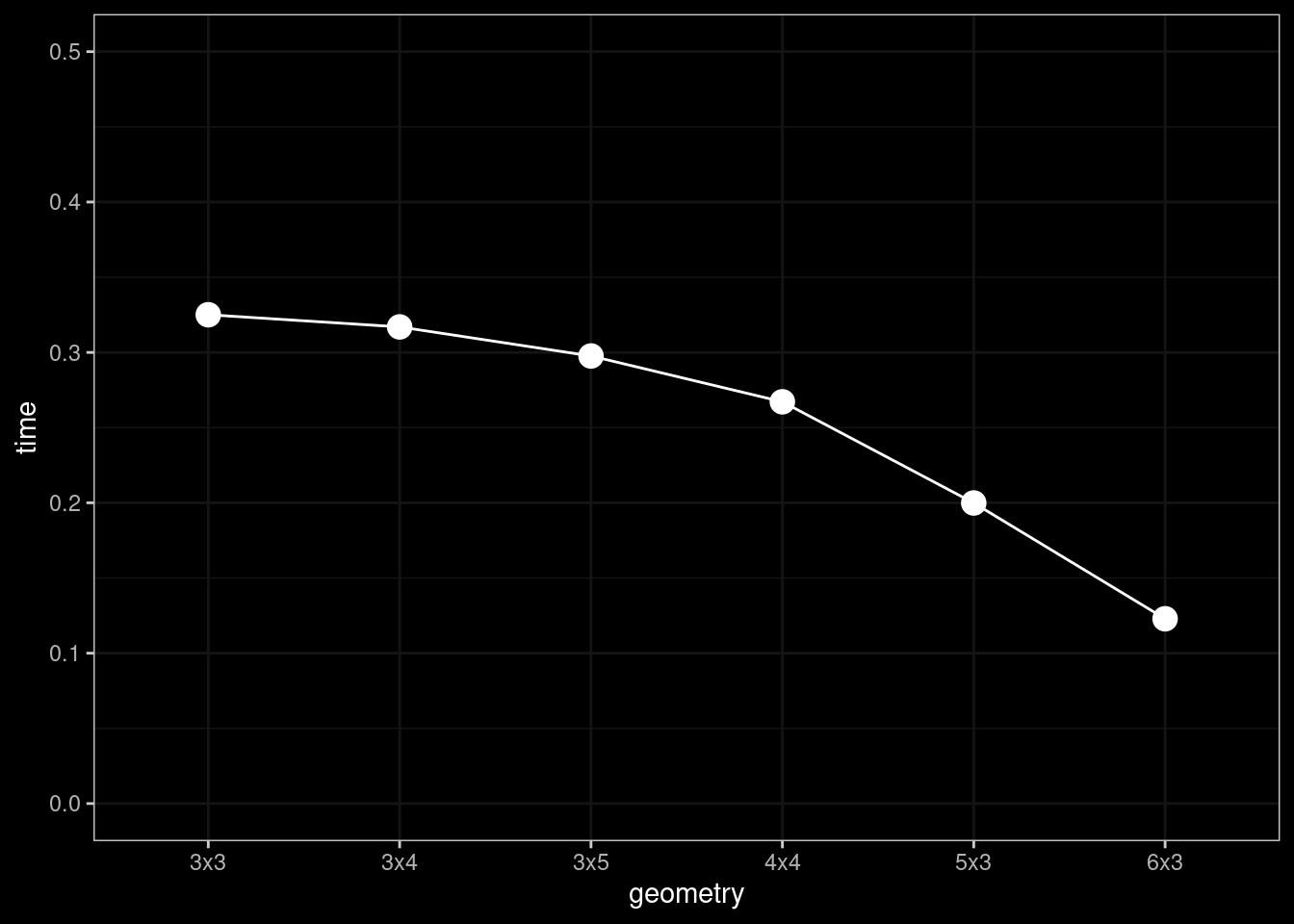
We see that the larger geometries have shorter evaluation times, which makes logical sense: time-per sub-board is relatively stable, but the larger geometries have fewer unique evaluations. However, optimizing for time, the larger overhead will likely be the application of the vision model, so that the relatively small time-differences is a minor issue in comparison.

4.3 Optimal Strategies

Arcade

For the arcade version of the game it is clear that we should use the geometry which optimizes the expected score per move, as the only constraint we have here is that we have 100 moves to complete the game.

Time Mode

Playing X-mas-3 via the graphical user interface adds significant overhead because of the image processing needed. However playing a series of pre-defined moves on the board has relatively low overhead. This suggests a strategy that will optimize the number of playable moved on the board per unit time.

 /\___/\
 \ -.- /
 `-.^.-'
   /"\      

Be afraid, Chris. Be very afraid...